Although we’ve already discussed isosceles triangles a bit during our discussion of 45-45-90 (i.e. isosceles right) triangles, it’s worth discussing some other contexts in which you may see isosceles triangles on the GMAT, specifically on Data Sufficiency problems.
As we discussed before, an isosceles triangle is any triangle that features two equal sides and thus two equal opposite angles:
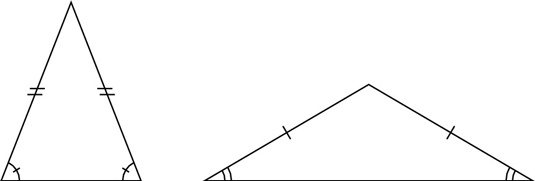
That’s an easy enough definition to remember, but how does the GMAT turn this into more challenging problems? For that, let’s take a look at the following Official Guide problem. Try to solve before reading the explanation below the problem:
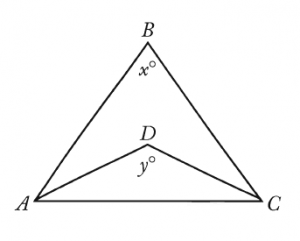
In the figure above, what is the value of x + y ?
(1) x = 70
(2) ABC and ADC are both isosceles triangles
Explanation
In this case, it’s straightforward enough to determine that each statement alone will be insufficient. Statement (1) gives us a definitive value for x, but no information about y, thus we cannot answer the question (the value of x+y). And although Statement (2) labels each triangle in the diagram as isosceles, we have no way of knowing the specific angles involved nor their relationships.
However, as with many Data Sufficiency problems, especially those involving Geometry, things can get thorny when we have to combine the statements. The two statements look very complimentary, and that could lead us to prematurely conclude the answer is C (i.e. the two statements are sufficient when combined). But we must do a thorough check.
Reframing the Question
Remember that at any point during a Data Sufficiency problem — beginning, middle, or end — you can reframe the question for simplicity. The question asks for the value of x+y. But now that we are combining the statements, we already know that x=70. In terms of sufficiency, then, what information do we need? The only thing missing is a definitive value of y. The question now might as well be “What is the value of y?”
Now, here’s where the GMAT thinking really comes into play. It’s one thing to understand what an isosceles triangle is. It’s quite another to judge what a diagram of an isosceles triangle does or does not tell you and what you can or cannot extrapolate from it.
One of my personal favorite things about Geometry Data Sufficiency problems is that they tend to be very intuitive visually. You can often answer them by manipulating figures.
We know that triangle ADC is isosceles, but is that enough to give us definitive measurements? Visually, which of these does it look like?
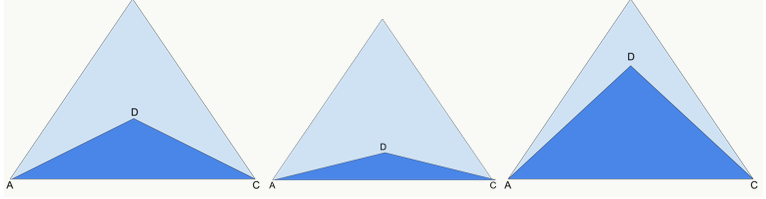
Without any numerical evaluations, we can see that we can’t get a definitive measure for the angle at D, which in this case is our y. So even when we combine the statements, we cannot get an answer to our question. The correct answer is E.
Here’s another case of a tricky Data Sufficiency problem involving isosceles triangles:
In isosceles triangle RST, what is the measure of angle R?
- The measure of angle T is 100 degrees
- The measure of angle S is 40 degrees
Again, give the problem a shot before reading the answer and explanation.
Explanation
This is one for which you can draw a diagram, but it’s not necessary. The trick here is to remember another key property of triangles, namely that all angles in the triangle must sum to 180 degrees.
Since the triangle is isosceles, and since each statement gives you only one angle of three, the temptation can be to say that each statement is insufficient on its own. This is certainly the case for Statement (2), because the 40-degree angle could be one of a pair (in which case we would have a 40-40-100 triangle) or the 40-degree angle could be the odd angle out (in which case we would have a 40-70-70 triangle).
Because the problem asks for the value of R, and since R could be 40, 70, or 100 depending on the situations outlined above, Statement (2) is INSUFFICIENT.
However, there’s a catch when evaluating Statement (1). Notice that angle T is an obtuse angle, meaning it is greater than 90 degrees. Is it possible that there are two 100-degree angles in a triangle? This would produce a total of 200 degrees, which would exceed the 180-degree total for any triangle. As such, the only possibility is that the 100 degree angle is the odd angle out, and the other two angles are equal acute angles (specifically, we have a 40-40-100 triangle).
Now we know R must be 40 degrees. Statement (1) is sufficient, and the correct answer is A.
But notice how the GMAT sets the statements up to bait you into thinking that you must combine the two statements to figure out the value of angle R.
Now that we’ve finished talking about the basic triangle types, we can move on to talking about what happens when triangles are used within different shapes. In the meantime, here are links to our other triangle articles:
A Short Meditation on Triangles
The 30-60-90 Right Triangle
The 45-45-90 Right Triangle
The Area of an Equilateral Triangle
Triangles with Other Shapes
Isosceles Triangles and Data Sufficiency
Similar Triangles
3-4-5 Right Triangle
5-12-13 and 7-24-25 Right Triangles
