As promised, we will now connect the 30-60-90 triangle to the equilateral triangle, specifically its area. There is a formula for the area of an equilateral triangle as it relates to the length of its side s, and it is as follows:
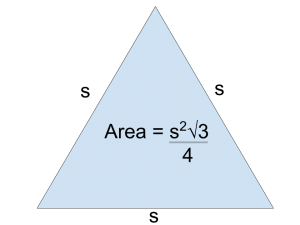
But more likely than not for the GMAT, you’ll need to understand how this formula is derived. And the √3 term in the area is a big clue.
First, it helps to remember that an equilateral triangle has all equal angles as well as all equal sides. And given that the angles in a triangle must sum to 180 degrees, each angle must be 60 degrees:
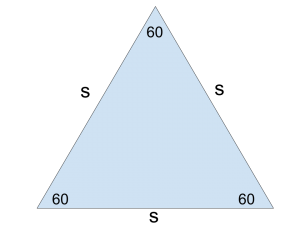
Now, what happens when we take such a triangle and split it down the middle?
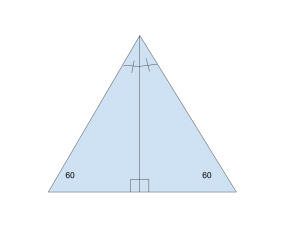 This should look familiar. Because the line segment down the middle acts as an angle bisector, the 60 degree angle at the top vertex becomes two 30-degree angles. Take a moment to consider what this produces and what the implications are.
This should look familiar. Because the line segment down the middle acts as an angle bisector, the 60 degree angle at the top vertex becomes two 30-degree angles. Take a moment to consider what this produces and what the implications are.
As you might have guessed, this line segment produces two 30-60-90 right triangles:
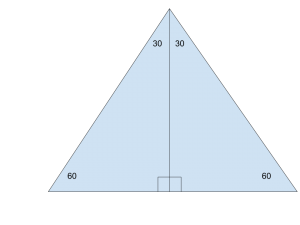
Not only that, but we can then use s to denote the side length of the equilateral triangle and map out each segment of the 30-60-90 right triangles. Before viewing the diagram below, take a moment to consider what the height of the triangle would be.
Remember that the ratio of side lengths is 1 : √3 : 2. If we fill in all of the appropriate lengths, we would get the following:
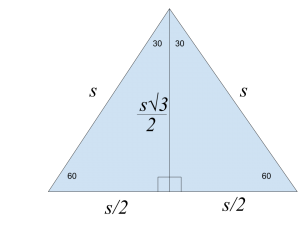 Now, we’re very close to deriving the area of the triangle, which is simply base*height/2. In this case, the base is s, while the height is s√3/2.
Now, we’re very close to deriving the area of the triangle, which is simply base*height/2. In this case, the base is s, while the height is s√3/2.
This is how we finally get the universal formula for an equilateral triangle:
Area = base * height / 2
Area = (s) * (s√3/2) / 2
Area = (s) * (s√3/4)
Area = (s2√3) / 4.
Now that we’ve seen the relationship between equilateral and 30-60-90 triangles, let’s see how it plays out in an official GMAT problem:
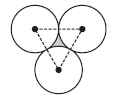
The figure shown above consists of three identical circles that are tangent to each other. If the area of the shaded region is 64√3 – 32π, what is the radius of each circle?
A. 4
B. 8
C. 16
D. 24
E. 32
Using signals
This is a complex problem that seems intimidating at first. However, if we use signals the problem is giving us, we can get to the answer more quickly than we might initially think. What signals does the area of the shaded region give us? Think about it before reading on…
If we look closely at the diagram, we see that an equilateral triangle is involved. We know this because each side of the triangle consists of two radii of each circle (i.e. the distance from the center to the outer edge of the circle), thus each side of the triangle must be equal. That’s a big hint that the √3 term is linked to the area formula we’ve been talking about.
Likewise, although it is not the subject of this post, the term using π is associated with circles in this case, the areas of the identical circles. (For reference, the area of a circle is πr2, and the circumference of a circle is 2πr.)
Conceptually, we should be able to see that 64√3 – 32π represents the area of the equilateral triangle minus the area of the three small sectors from the circles.
Now, rather than do any unnecessarily complicated math, we should take notice that the question asks for the radius of each circle, and each side of the equilateral triangle is 2r:

We already know that the area of the equilateral triangle is 64√3, and we have the formula for that area, so we are just a few steps away from solving for the radius.
Remember the formula, where s is the length of the side of the equilateral triangle:
Area = (s2√3) / 4
Substitute:
64√3 = (s2√3) / 4
Since √3 is common to both sides, you can divide it out:
64 = s2 / 4
256 = s2
Now, normally, you would say that s could be 16 or -16, but since this is a geometric quantity, we only deal in nonnegative quantities. Therefore:
s = 16, giving us the length of each side of the equilateral triangle.
Be careful, however. This could trap you into picking answer choice C. Remember to check exactly what the question asks for. We were asked for the radius of the circle, which as we see in the above diagram is half the length of s. The correct answer is B.
Again, it’s very important to notice that we didn’t do anything with the circles. The 64√3 term and the equilateral triangle were enough to get us the length of each side and thus the radius. Look for signals to help short-circuit problems and avoid lengthy solution paths.
Now that we’ve reviewed all of the basic triangles, we’ll do a little more next time on how triangles can appear in other shapes, such as circles and rectangles. We got a little taste today, so hopefully that will give you a good idea.
Find more articles in our triangle series here:
A Short Meditation on Triangles
The 30-60-90 Right Triangle
The 45-45-90 Right Triangle
The Area of an Equilateral Triangle
Triangles with Other Shapes
Isosceles Triangles and Data Sufficiency
Similar Triangles
3-4-5 Right Triangle
5-12-13 and 7-24-25 Right Triangles
By: Rich Zwelling, Apex GMAT Instructor
Date: 14th January, 2021
