Right Triangle Identities: 3-4-5
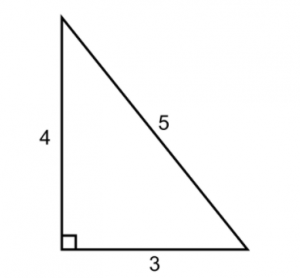
 Right triangles always adhere to the same basic relationship, reflected by the Pythagorean Theorem, or a² + b² = c², where a, b, and c match the triangle sides as pictured above. c always represents the longest side, called the hypotenuse.
Right triangles always adhere to the same basic relationship, reflected by the Pythagorean Theorem, or a² + b² = c², where a, b, and c match the triangle sides as pictured above. c always represents the longest side, called the hypotenuse.
But rather than use the formula directly, the most common way the GMAT will test knowledge of the formula is through the simplest integer values that fit this relationship. The most common is 3² + 4² = 5² → 9 + 16 = 25, as pictured below:
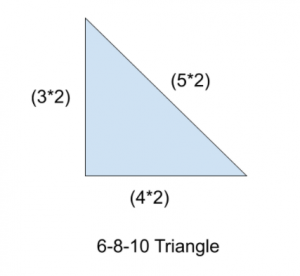
What’s important to remember is that this relationship works not only for 3-4-5, but also for any corresponding multiples, such as 6-8-10 or 9-12-15 or any other multiples of the original numbers.
GMAT Triangle Problem #1
If you rely solely on the formula, you could certainly get the job done, but it will take you a lot longer. Here’s an Official Guide problem that drives this point home:
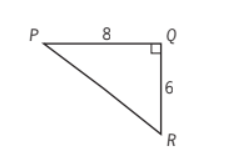 The figure above shows a path around a triangular piece of land. Mary walked the distance of 8 miles from P to Q and then walked the distance of 6 miles from Q to R. If Ted walked directly from P to R, by what percent did the distance that Mary walked exceed the distance that Ted walked?
The figure above shows a path around a triangular piece of land. Mary walked the distance of 8 miles from P to Q and then walked the distance of 6 miles from Q to R. If Ted walked directly from P to R, by what percent did the distance that Mary walked exceed the distance that Ted walked?
(A) 30%
(B) 40%
(C) 50%
(D) 60%
(E) 80%
If you know your so-called “Pythagorean Triples” from memory (e.g. 3-4-5, 6-8-10), this problem moves along much faster. By test day, you should know within seconds that segment PR is length 10, no calculations involved.
After that, the bulk of your time should be spent calculating the percent difference between Mary’s total distance (14) and Ted’s total distance (10). (Answer: Since Mary walked 4 more miles more than Ted’s original 10, and 4 is 40% of 10, this makes B the correct answer.)
GMAT Triangle Problem #2
Also, it’s much more likely that the GMAT will test your knowledge of completeness of information with respect to Right Triangles, especially on Data Sufficiency. Give this problem a shot before reading on:
 What is the area of triangle ABC pictured above?
What is the area of triangle ABC pictured above?
- The length of segment AB is 5
- The perimeter of triangle ABC is 12
A) Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
B) Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
C) BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
D) EACH statement ALONE is sufficient to answer the question asked.
E) Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
If you know your 3-4-5 Pythagorean triple really well, you may prematurely view Statement (1) as sufficient, since you may believe the hypotenuse of 5 automatically guarantees the legs of the triangle must be 3 and 4. But this assumes the legs must have integer lengths. In reality, the legs could be any non-integer lengths that satisfy a² + b² = 5².
This is a classic way the GMAT could throw you off your guard. And it’s another way to test that only one side of a triangle is not enough to give you complete information about the entire triangle. Statement (1) is actually INSUFFICIENT, because we do not have information about a unique triangle, and thus could not possibly know the area.
Likewise, Statement (2) is INSUFFICIENT, because there are many ways to generate a right triangle with a perimeter of 12.
When we combine the statements, however, it’s interesting to note that, as a rule, we know we have a unique triangle if we’re given both the perimeter and the hypotenuse. As such, we would be able to find the area (even though we don’t have to calculate it), and thus the answer is C. Don’t do any math!
Takeaways
The big takeaway here is that, rather than have you use the Pythagorean theorem directly, the GMAT will try to force you into false conclusions, such as believing a hypotenuse of 5 gives you all the information you need. Be on your toes! Make sure to thoroughly examine all information given to you!
The 3-4-5 triangle is not the only identity to review in this triangle geometry section, here are some other identities and triangle related topics to review:
A Short Meditation on Triangles
The 30-60-90 Right Triangle
The 45-45-90 Right Triangle
The Area of an Equilateral Triangle
Triangles with Other Shapes
Isosceles Triangles and Data Sufficiency
Similar Triangles
3-4-5 Right Triangle
5-12-13 and 7-24-25 Right Triangles
Triangle Inequality Rule
