If you’re preparing for Quantitative Reasoning on the GMAT, mastering prime factorization can give you a significant edge. This article explains prime factorization concepts, application, and provides practical tips to enhance your problem-solving skills. By understanding and applying prime factorization techniques, you’ll be better equipped to navigate the quantitative section with confidence and precision.
What Is Prime Factorization?
Prime factorization is an important concept in number theory that is tested on the quantitative section of the GMAT. It involves expressing a positive integer as a product of prime numbers, which are numbers that have exactly two factors: 1 and the number itself. The test will challenge your ability to break down integers to their prime factors. Integers are a class of numbers sometimes referred to as “whole numbers.” Integers can be positive, negative, or 0 in value, and you can write them without using fractions or decimals.
Integers Non-Integers
17 83.35
-460 76/45
0 -⅙
The First 15 Prime Numbers: Starting at the Base
Again, a prime number is an integer that is not divisible by any integers other than itself and 1. It’s worth pointing out that every integer is divisible by itself and 1. Every number, whether it’s an integer or not, is divisible by itself, since x/x = 1. (The case of 0/0 is best left to professional mathematicians; it won’t appear on the GMAT.) Dividing any number, whether it’s an integer or not, by 1, effectively does nothing, just as multiplying any number by 1 effectively does nothing. x/1 = x, and x*1 = x. Here are the first 15 prime numbers, the ones occurring between 1 and 50: 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 Try dividing any of these numbers by an integer other than itself or 1, and your quotient won’t be an integer. (If you’re curious why these and not any other integers represent the first 15 primes, you’ll have a hard time finding an explanation, because a mathematically provable model for describing or predicting the series of prime numbers remains one of the most elusive mysteries in mathematics.) Note that every prime number except for 2 is odd. With this understanding of prime numbers, you’d see them as the “building blocks” of an integer. They are the fundamental elements that cannot be divided further. Let’s use some official GMAT problems to practice the process of reducing integers to their prime factors. We refer both to this process and to the resulting list of primes as the “prime factorization” of the integer.
Perfect Squares and Their Prime Factors
Let’s take a look at perfect squares and their prime factors. Perfect squares are numbers you get by squaring an integer, indicated by an exponent of 2. For example: 5^2=25 The square root is the integer you use to create a perfect square. For example, the square root of 25 is 5. Non-perfect squares also have square roots, but these roots are not integers, like the square root of 2 being approximately 1.41. Negative numbers do not have real square roots since squaring any real number, positive or negative, results in a positive number.
The 2 Main Methods of Prime Factorization
Prime Factorization by Division
An integer’s prime factors are the prime numbers that, when multiplied together, produce the integer. A prime number is an integer that is not divisible by any integers other than itself and 1. Divisibility means that when an integer is divided by another integer, the result (called the quotient) is also an integer. Here are some examples: 56 / 7 = 8 → 56 is divisible by 7 56 / 6 = 9.33 → 56 is not divisible by 6 132 / 12 = 11 → 132 is divisible by 11 132 / 15 = 8.8 → 132 is not divisible by 15 65 / 13 = 5 → 65 is divisible by 13 65 / 8 = 8.125 → 65 is not divisible by 8 If integer n is divisible by integer x, then integer x is called a divisor of integer n. Integer x may also be called a factor of integer n. The term “divisor” is, of course, related to the operation of division, and the term “factor” is related to the operation of multiplication. Relationships between integers may be spoken of in terms of either division or multiplication. These represent two interchangeable ways of speaking about integers. If we want to speak in terms of multiplication, then instead of saying that integer n is divisible by integer x, we say that integer n is a multiple of integer x. This means that there is some integer by which x can be multiplied to produce n. Here are the same examples from before, this time in terms of multiples. 56 / 7 = 8 → 56 is a multiple of 7 (and a multiple of 8) 56 / 6 = 9.33 → 56 is not a multiple of 6 132 / 12 = 11 → 132 is a multiple of 12 (and a multiple of 11) 132 / 15 = 8.8 → 132 is not a multiple of 15 65 / 13 = 5 → 65 is a multiple of 13 (and a multiple of 5) 65 / 8 = 8.125 → 65 is not a multiple of 8 Note the parentheticals: we could rearrange the values to say 56 / 8 = 7 or 132 / 11 = 12 or 65 / 5 = 13. To generalize this principle, if integer n is a multiple of integer x, then integer n is also a multiple of whatever integer, when multiplied by x, produces n.
5 Different Ways to Ask the Same Question About 2 Integers
Is n divisible by x? Is n a multiple of x? Is x a divisor of n? Is x a factor of n? Is n/x an integer? As you prepare to take the GMAT, you will see so many of these questions that you will be able to understand what is being asked without really noticing the changes in terminology. The goal is for your brain to develop a concept of divisibility that is readily identified by any of the above ways of speaking. The frequency of this concept on GMAT quant makes it hard to get a great score without knowing your multiplication table like the back of your hand. If there are any two integers between 1 and 12, inclusive, whose product (the result when these integers multiply each other) you don’t know instantly, it’s time to review your multiplication table and possibly whip out the flash cards. As elementary as this feels, it will serve you well.
Prime Factorization by Factor Tree
Here’s a GMAT problem to solve using the factor tree method. The “prime sum” of an integer n greater than 1 is the sum of all the prime factors of n, including repetitions. For example, the prime sum of 12 is 7, since 12 = 2 * 2 * 3 and 2 + 2 + 3 = 7. For which of the following integers is the prime sum greater than 35? (A) 440 (B) 512 (C) 620 (D) 700 (E) 750 This problem is helpful because it includes an example of prime factorization with the integer 12. There are two possible “routes” for us to perform the prime factorization of 12. We can work through and display these “routes” with a factor tree tool.
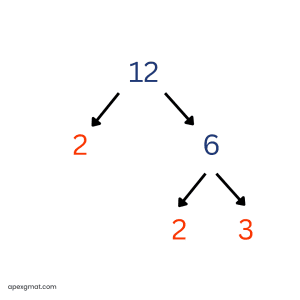
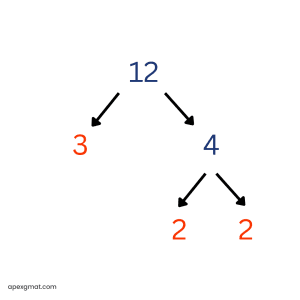
When we perform a prime factorization of an integer, we “break down” the number into sets of factors until all of the factors are prime and cannot be broken down further. With the integer 12, we may begin with the factor pair of 2 * 6 or with the factor pair of 3 * 4. In the first case, we finish by breaking the 6 into 2 * 3. In the second case, we finish by breaking the 4 into 2 * 2. Either way, the resulting prime factorization of 12 is 2 * 2 * 3. (I like to underline the prime factors as I find them in order to keep track.) No matter which “route” is taken in the prime factorization of an integer, the resulting list of prime factors is always the same. It is often helpful to group repetitions of the same prime factor using exponents. So for 12, instead of “2 * 2 * 3,” we can express the prime factorization as “22 * 3.” In this problem, we are looking for the number whose “prime sum” – or, as we are told, the sum of all its prime factors – is greater than 35. If you know your first 15 prime numbers, a certain answer choice here jumps out. But for the sake of learning and practice, we will prime factorize each answer choice and check its prime sum. Here’s answer choice A:
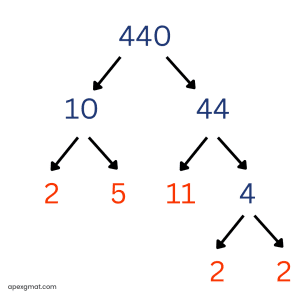
Prime factorization: 23 * 5 * 11 Prime sum = 2 + 2 + 2 + 5 + 11 = 24 When an integer ends with one or more 0s (as 440 does), it’s best to begin by isolating the factors of 10, each of which breaks into the prime factors of 2 and 5. Here’s how this would work for a larger integer: 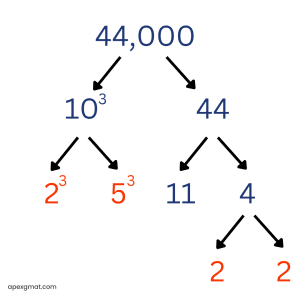
The prime sum for 440 was 24, which is too low, so we’ll have to move on to answer choice B: 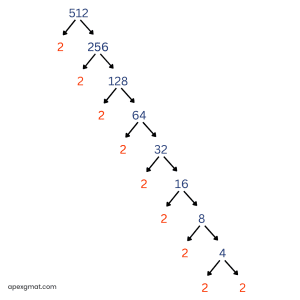
This is a prime example (pun intended) of why you should memorize some powers of 2, 3, 5, and 6 along with your multiplication table! When you see a number like 512, it can be a big time-saver to know immediately, “Oh, that’s 29.” The prime factorization of 512 is 29, and its prime sum is 18. This is too low, so we’ll move on to answer choice C:
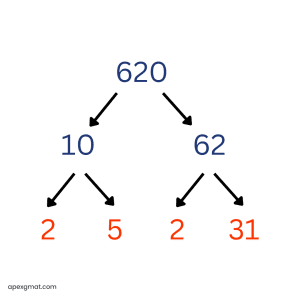
Prime factorization: 22 * 5 * 31 Prime sum: 2 + 2 + 5 + 31 = 40 C is the correct answer because 620 contains the prime factor 31, virtually guaranteeing that the prime sum is greater than 35. (Given the importance of primes on GMAT quant, perhaps it is no coincidence that the section contains 31 questions.)
Anatomy of a GMAT Prime Factorization Problem
We’ll continue with the following Official Guide GMAT problem to talk about the anatomy of GMAT Prime Factorization. Give the problem a shot, if you can: How many prime numbers between 1 and 100 are factors of 7,150?
- A) One B) Two C) Three D) Four E) Five
One of the things you’ll notice is the linguistic setup of the problem, which is designed to confuse you immediately (a common theme in GMAT problems). They get you panicking right away with the mention of a large range (between 1 and 100), and then they compound your frustration by giving you a rather large value (7,150). Don’t let that convince you that you can’t solve the problem. Remember, the GMAT is not interested in large calculations or memorization involving large numbers. Chances are, if you find yourself thinking about a complicated way to solve a problem, you’re taking the wrong approach, and there’s a simpler way. Try to pick out the most operative signal words, which let you know how to address the problem. We are dealing with prime numbers and also the topic of finding factors. The language of the problem may make you nervous, thinking that we must consider a slew of prime numbers up to 100. But the only primes we are really interested in are those that are actually factors of 7,150. So let’s focus our attention there. And we can do so with a prime factor tree, as described earlier. Now, in the case of 7,150 we don’t have to break it down into prime numbers immediately. Split the number up into factors that are easy to recognize. In this case, the number ends in a zero, which means it is a multiple of 10, so we can start our tree like this: 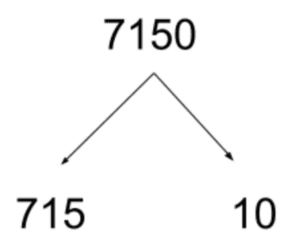
Notice that the advantage here is two-fold: It’s easier to divide by 10 and the two resulting numbers are both much more manageable. Splitting up 10 into its prime factorization is straightforward enough (2 and 5). However, how do we approach 715? Well, since it ends in a 5, we know it must be divisible by 5. At that point, you could divide 715 by 5 using long or short division… …or you could get sneaky and use a NARRATIVE approach with nearby multiples: 750 is nearby, and since 75/5 = 15, that must mean that 750/5 = 150. Now, 750 is 35 greater than 715. And since 35/5 = 7, that means that 715 is seven multiples of 5 away from 750. So we can take the 150, subtract 7, and get 143. Mathematically, you can also see this as: 715/5 = (750-35)/5 = 750/5 – 35/5 = 150 – 7 = 143 So as stands, here’s our GMAT prime factorization:
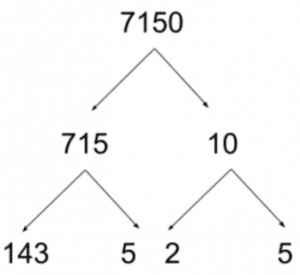
Now, there’s just the 143 to deal with, and this is where things get a bit interesting. There are divisibility rules that help make factoring easier, but an alternative you can always use is finding nearby multiples of the factor in question. For example, is 143 divisible by 3? There is a rule for divisibility by 3, but you could also compare 143 against 150. 150 is a multiple of 3, and 143 is a distance of 7 away. 7 is not a multiple of 3, and therefore 143 is not a multiple of 3. This rule applies for any factor, not just 3. Now we can test the other prime numbers. (Don’t test 4 and 6, for example. We know 143 is not even, so it’s not divisible by 2. And if it’s not divisible by 2, it can’t be divisible by 4. Likewise, it’s not divisible by 3, so it can’t be divisible by 6, which is a multiple of 3.) 143 is not divisible by 5, since it doesn’t end in a 5 or 0. It’s not divisible by 7, since 140 is divisible by 7, and 143 is only 3 away. What about 11? Here you have two options:
- Think of 143 as 110+33, which is 11*10 + 11*3 → 11*(10+3) → 11*13
- If you know your perfect squares well, you could think of 143 as 121+22
→ 11*11 + 11*2 → 11*(11+2) → 11*13 Either way, you should arrive at the same prime factorization: 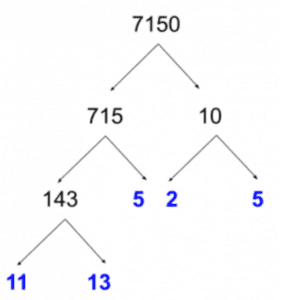
Notice that I’ve marked all prime numbers in blue. This result shouldn’t be a surprise, because notice that everything comes relatively clean: there are only a few prime numbers, they are relatively small, and there is just one slight complication in solving the problem (the factorization of 143). So what is the answer? Be very careful that you don’t do all the hard work and falter at the last second. There are five ends to branches in the above diagram, which could lead you prematurely to pick answer choice E. However, two of these branches have the same number (5). There are actually only four distinct primes (2, 5, 11, 13). The correct answer is D. Again, notice that the range given in the question stem (1 to 100) is really a linguistic distraction to throw you off track. We don’t even go beyond 13. Now, that was easy. Let’s go one level up.
Try Out This Official GMAT problem
Here are the prime factorizations of answer choices D and E, just for practice:
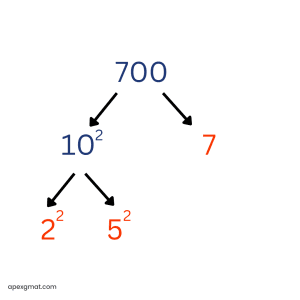
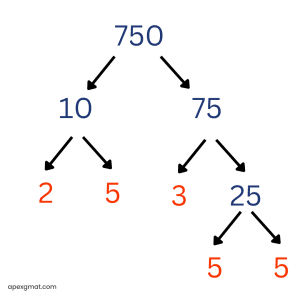
Prime factorization is one of the easiest GMAT quant skills to practice because you can use any integer that comes to mind! Let’s try another official GMAT problem: How many prime numbers between 1 and 100 are factors of 7,150? (A) One (B) Two (C) Three (D) Four (E) Five This is a very straightforward problem. Just prime factorize 7,150 and see how many different prime factors there are. 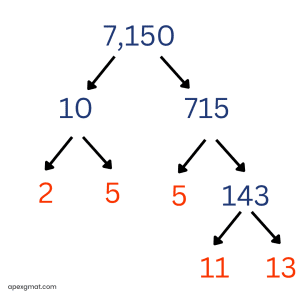
Straightforward, but easier said than done. If you got stuck trying to divide 715, you can always use an “obvious factor” like 5. Since 715 has a units digit of 5, we know that it is divisible by 5. Then all you need is the quotient of 715 / 5. Dividing 143 is a little trickier, since it has no obvious factors. If you mistakenly conclude that 143 is itself a prime factor, you will choose incorrect answer choice B for this problem. Sharp factoring eyes will notice that 143 = 130 + 13, or 11 * 13. We can count four different prime factors of 7,150 (2, 5, 11, and 13), so the correct answer choice is D. If this was challenging for you, remember, you can practice with any integer. Here’s a final problem for this article: If 3 < x < 100, for how many values of x is x/3 the square of a prime number? (A) Two (B) Three (C) Four (D) Five (E) Nine The initial step to solving this problem is less obvious. We want to know how many integers greater than 3 and less than 100 are divisible by 3 and then by the square of a prime number, with no further prime factors. The only values that can work are the multiples of 3 (since these are the only values divisible by 3), but there are too many multiples of 3 between 3 and 100 to check! The best way to proceed is to reverse the process. Square a prime, multiply your result by 3, and see if this final product is less than 100. 22 * 3 = 12 Hey, we know this one from before. Let’s keep going: 32 * 3 = 9 * 3 = 27 52 * 3 = 25 * 3 = 75 72 * 3 = 49 * 3 = 147 This is already too high, so only three values (12, 27, and 75) satisfy the conditions specified in the problem. The correct answer choice is B.
Master Prime Factorization with an Apex Tutor
By choosing to master prime factorization with an Apex tutor, you invest in a structured, efficient, and personalized learning experience that maximizes your potential and sets you up for success on the GMAT. You won’t only master prime factorization but also develop other essential skills needed for the GMAT. This holistic preparation is crucial for achieving a high score. Talk to our team of experts today to start your GMAT prep journey.
Frequently Asked Questions about Prime Factorization
1. How to do prime factorization?
To find the prime factorization of a number, follow these steps:
- Divide the number by the smallest prime factor possible.
- Repeat step 1 with the resulting quotient until the quotient becomes 1.
- Write the number as a product of all the prime factors found in steps 1 and 2.
Watch this video and test what you’ve learned.
2. What is the prime factorization of 100?
The prime factorization of 100 is 2² × 5²: 100 ÷ 2 = 50 50 ÷ 2 = 25 25 ÷ 5 = 5 5 ÷ 5 = 1 100 = 2 × 2 × 5 × 5 = 2² × 5²
3. What is the prime factorization of 24?
The prime factorization of 24 is 2³ × 3. 24 ÷ 2 = 12 12 ÷ 2 = 6 6 ÷ 2 = 3 3 ÷ 3 = 1 24 = 2 × 2 × 2 × 3 = 2³ × 3
4. What are the prime factors of 50?
The prime factors of 50 are 2 and 5 50 ÷ 2 = 25 25 ÷ 5 = 5 5 ÷ 5 = 1 50 = 2 × 5 × 5 = 2 × 5²
