Perfect squares are an essential concept in GMAT quantitative reasoning. Understanding their properties, particularly in light of their prime factors, can help you tackle a variety of problems on the GMAT.
In this article, we’ll explore the concept of perfect square factors and discuss some key properties that frequently appear on the GMAT.
What are Perfect Squares?
Perfect squares are integers that result from multiplying an integer by itself. This operation is called “squaring” and is denoted by an exponent of 2. For example:
- 5² = 25
- 11² = 121
- 17² = 289
The integer that is squared to produce the perfect square is called its square root. So, 5 is the square root of 25, 11 is the square root of 121, and 17 is the square root of 289.
Non-Perfect Squares
Numbers that are not perfect squares have square roots too, but their square roots are not integers.
For example, the square root of 2 is approximately 1.41. Since 1.41 is not an integer, 2 is not a perfect square. Similarly, the square root of 3 is about 1.71, indicating that 3 is not a perfect square.
Positive and Negative Square Roots
Another important property of perfect squares is that they have both positive and negative square roots. For example, both 9 and -9 are square roots of 81 because 9 x 9 = 81 and -9 x -9 = 81. The only exception is 0, which has only one square root: 0.
This property is often tested on the GMAT, especially when factoring quadratic equations.
Prime Factors of Perfect Squares
In the multiplication table below, the first 20 perfect squares form the diagonal line highlighted in yellow: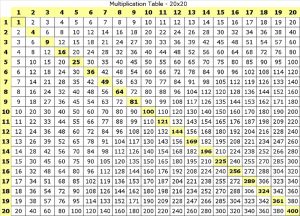
For GMAT quant, it’s helpful to know this series of numbers. Perfect squares are an important topic on GMAT quant, and one frequently tested property is that perfect squares have prime factors in pairs. In other words, if a perfect square has a certain prime factor, it has an even number of that prime factor.
In the prime factorization of the perfect square, all of the exponents used to notate the number of occurrences of each prime factor are even. Let’s look at an example:
If x is an integer and x² = 150*n, what is the smallest possible value that n can take?
Here we’re given a seemingly complex problem, which is simple once we break it down. Since we have two “copies” of x, we must have two pairs of each of x’s prime factors. The hint is in the 150.
We can prime factorize 150 into 2*3*5*5. Since 150 has a prime factor of 2, this means that x must contain 2. Since there are two xs, the n must contain the second copy of 2. The same goes for 3. Since there are two 5s, we have enough 5s to make this work. A picture, in this case an equation, is worth a thousand words
x * x = 150 * n
x * x = 2*3*5*5 * n
x = 2 * 3 * 5 = 30 So a single x must have at least 2, a 3, and a 5.
x * x = (2*_) * (3*_) * (5*5) ← we’re “missing” a 2 and a 3 to have all the prime factors paired off. Remember, we need two copies of each, one for each x.
So n = 2*3, and x² = 900.
Why Must Prime Factors Be Paired?
A perfect square must have an even number of prime factors of 2. It can have zero (not divisible by 2), or two, four, six, twelve, five hundred factors of 2, but it cannot have, for example, five prime factors of 2.
If an integer has an odd number (uneven number) of some prime factor, it will be impossible to evenly split the occurrences of this prime factor into two groups. Therefore, the integer in question cannot be the product of two equal integers – also known as the square of an integer.
Let’s Explore This With an Official GMAT Problem:
If y is the smallest positive integer such that 3,150 multiplied by y is the square of an integer, then y must be:
(A) 2
(B) 5
(C) 6
(D) 7
(E) 14
In order to make a perfect square, we need even numbers of each prime factor. Therefore if 3,150 has odd numbers of one or more prime factors, we need y to contain the “missing” primes such that 3,150 * y has even numbers of these prime factors. If this doesn’t make sense, observing the prime factorization of 3,150 may help.
3,150 = 2 * 32 * 52 * 7
3,150 has a pair of 3s and a pair of 5s, but only one prime factor of 2 and one prime factor of 7. This means that there is no way to split the prime factors of 3,150 into two identical groups.
Therefore, 3,150 is not the product of two identical integers, i.e., not the square of an integer.
What prime factors are “missing” in order to make this possible? We need at least one more prime factor of 2 and one more prime factor of 7. Therefore, in order for 3150 * y to be the square of an integer, y must have at least one prime factor of 2 and one prime factor of 7. The only answer choice that satisfies this condition is (E) 14. No lower number can work.
Another property of the factors of perfect squares is tested in the following official problem:
If 2^(x+y) = 4^8 , what is the value of y?
- x^2 = 81
- x – y = 2
(A) Statement (1) alone is sufficient, but statement (2) alone is not sufficient.
(B) Statement (2) alone is sufficient, but statement (1) alone is not sufficient.
(C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
(D) EACH statement ALONE is sufficient.
(E) Statements (1) and (2) TOGETHER are not sufficient.
Some knowledge of exponents helps make sense of this problem. We can apply a “change of base” to 48:
2^(x+y) = 4^8
2^(x+y) = (2^2)^8
2^(x+y) = 2^16
x + y = 16
This simplifies the equation we are given in the question stem. It is unnecessary to perform these steps to answer the problem correctly – you could simply count the variables and the equations. Since there are two variables, x and y, a system of two different equations relating to these variables will be sufficient to solve both variables. The question stem supplies one such equation, and statement 2 supplies another.
Therefore, statement 2 by itself is sufficient. But what about statement 1 by itself?
If you said that statement 1 by itself is sufficient because it supplies the value of x (x = 9) such that the value of y can also be determined using the equation in the question stem, you probably forgot about a property of the factors of perfect squares. If x2 = 81, then yes, x could equal 9, the positive square root of 81. But x could also equal -9, the negative square root of 81. 9 * 9 = 81, and -9 * -9 = 81. Unless we are told in some way that x is positive – and in this problem, we aren’t told this – either value is possible. If there are two possible values for x, then there are two possible values for y, and statement 1 by itself is insufficient.
Note that x^2 doesn’t have to be a perfect square for this property to apply. Every positive number has both a positive and a negative square root. 0 has only one square root: 0.
Here’s a final official GMAT problem to check your comprehension of this “negative square root” property.
If k^2 = m^2, which of the following must be true?
(A) k = m
(B) k = –m
(C) k = |m|
(D) k = -|m|
(E) |k| = |m|
The correct answer is E. We don’t know about the positivity or negativity of either of the square roots k and m. But we know that if the squares of k and m are equal, k and m must be equal in absolute value.
Do you still find prime factors overwhelming? Consider working with a private GMAT tutor if you need additional help preparing for the GMAT. Apex tutors, have all scored over 770 on the GMAT and can provide personalized guidance and help you develop strategies for success on the exam.
Frequently Asked Questions on Perfect Square Factors
1. Why are perfect squares and their factors important for the GMAT exam?
Understanding the properties of perfect square factors is essential for success on the GMAT quantitative section.
Remember that perfect squares have prime factors in pairs and both positive and negative square roots (except for 0). Mastering these concepts will better equip you to tackle a variety of GMAT problems involving perfect squares.
2. How to know if a number is a perfect square?
To determine if a number is a perfect square, you can:
- Find its square root: If the square root is a whole number, then the original number is a perfect square.
- Use Prime factorization: If all prime factors in the number’s prime factorization have an even number of occurences, then the number is a perfect square.
3. What is the perfect square formula?
The perfect square formula states that:
(a + b)² = a² + 2ab + b²
In other words, when you square a binomial (an expression with two terms), the result is the sum of the squares of each term plus twice the product of the terms.
Let’s break down the formula:
- a² is the first terms multiplied together
- b² is the last terms multiplied together
- 2ab is the middle terms multiplied together twice (inners and outers)
The perfect square formula can be applied in various ways on the GMAT. Here are a few examples:
Identifying perfect squares and solving equations: If an expression matches the perfect square formula, you can quickly identify it as a perfect square. For example, if you see an expression like x² + 6x + 9, you can recognize it as a perfect square because it fits the formula (a + b)² with a = x and b = 3.
Factoring quadratic expressions: When you encounter a quadratic expression that is a perfect square, you can factor it using the perfect square formula. For example, 4x² + 20x + 25 can be factored as (2x + 5)².
