Understanding Exponents
A key piece of algebraic notation on GMAT and Executive Assessment (EA) quant problems is the exponent. Exponents appear on many kinds of quantitative problems, so fluency with exponents (and radicals) is an indispensable skill for achieving a competitive quant score. Odds are, you already have some idea of what exponents “mean” in algebraic language, but let’s clarify your definition by exploring how exponents relate to the more fundamental operations of addition and multiplication.
The foundations of all arithmetic are the operations of addition and subtraction. We could even say just addition, since subtraction can be notated as the addition of a negative value. Why have I left out multiplication and division? Well, because multiplication is nothing but an efficient way to notate a special case of addition, and division is nothing but multiplication in reverse. The special case of addition is this: when you want to add up a large number of groups that are all the same size. Let’s say you want to know how many eggs are in stock at your local grocery store. You won’t count the eggs one by one; you’ll count the cartons, since you know that each carton contains 10 or 12 eggs, depending if you’re in America or Europe. You could “show your work” for counting the eggs like this:
12 + 12 + 12 + 12 + 12 + 12 . . .
But this would get out of hand. Multiplication was created for just such a job. Instead of writing out the addition of 217 dozens of eggs, you can write this:
(# of eggs) = 217 * 12
This is many times better than stringing together 217 twelves with plus signs, but the outcome is the same.
The relevance to exponents is this: just as multiplication efficiently notates successive additions of the same value, exponents efficiently notate successive multiplications by the same value.
To stay in the realm of our “eggs at the grocery store” scenario, let’s imagine that a local farm starts out with 5 hens and wants to double its egg-laying workforce every year for the next 7 years. We could notate the target number of hens at the end of the seventh year like this:
5 * 2 * 2 * 2 * 2 * 2 * 2 * 2 = 640
But this is a bit impractical. In scenarios where the population of a bacteria doubles hundreds of times, notating with multiplication simply won’t do. We need a better tool, and the tool is exponents. Returning to our hen population example, exponents work like this:
5 * 2 * 2 * 2 * 2 * 2 * 2 * 2 = 640
5 * 2⁷ = 640
Rather than stringing together seven 2s with multiplication signs, we can place a 7 as an exponent of the 2 to notate the same thing. When we do this, the 2 is called the base of the exponential expression. The value represented by xⁿ is called the nth power of x or “x to the nth power. In the latter option, “power” is often left tacit, so in our hen scenario, we would verbalize the value of the final population as “five times two to the seventh (power)” or, for a slight simplification, “five times two to the seven” The terms squared and cubed are used for exponents of 2 and 3, respectively. 6² is “six squared”; 5³ is “5 cubed.”
This proper understanding of exponents as shorthand for multiplication makes sense of their properties. Many an algebra student has been tripped up by expressions like this:
x⁷ * x⁴
Seeing the multiplication sign, a novice might incorrectly infer that x⁷ * x⁴ = x²⁸ and be confused by the correction that the exponents should be added, not multiplied, yielding x¹¹. Breaking down the exponential expressions x⁷ and x⁴ to their “original” multiplicative forms should add clarity.
x⁷= x * x * x * x * x * x * x
x⁴ = x * x * x * x
x⁷ * x⁴ = (x * x * x * x * x * x * x) * (x * x * x * x) = x¹¹
Now we can see that the multiplication of the exponential expressions x⁷ and x⁴ is nothing but a chain of multiplications of the variable x: 11 of them, to be exact. And the best way to notate a string of eleven “x’s” in multiplication is with an exponent of 11.
The product of equal bases with different exponents is the base raised to the sum of the exponents. xᵃ * xᵇ = xᵃ⁺ᵇ
With this rule in place, it follows that it can be reversed by “splitting” an exponential expression into two groups.
x¹¹ = x⁷ * x⁴ = x⁶ * x⁵ = x¹⁰ * x
As shown, the way you “split” your expression is flexible. Different algebraic scenarios can benefit from different “splits.”
When the operation is division instead of multiplication, the resulting exponent is calculated via subtraction instead of addition.
x⁷ / x⁴ = (x * x * x * x * x * x * x) / (x * x * x * x)
(x * x * x * x * x * x * x) / (x * x * x * x) = x³
The quotient of equal bases with different exponents is the base raised to the difference of the exponents. xᵃ / xᵇ = x⁽ᵃ⁻ᵇ⁾
This covers multiplication and division of equal bases with different exponents. Simple rules also exist for multiplication and division of different bases with equal exponents.
x³ * y³ = (xy)³
Again, breaking down the exponential expressions to their “original” multiplicative forms shows why this works:
x³ * y³ = (x * x * x) * (y * y * y)
Everything here is in multiplication, so we can reorder and regroup the factors any way we like.
(x * x * x) * (y * y * y) = xy * xy * xy = (xy)³
Don’t forget the parentheses around your base. Note that we need the parentheses to group the xy as a unit, as opposed to xy³ = x * y*y*y.
Of course, this rule works in reverse as well.
(xy)³ = x³ * y³
Again, different algebraic scenarios call for different algebraic solutions. Both the combination and the “splitting” of algebraic expressions are useful tools in different contexts.
xᵃ * yᵃ = (xy)ᵃ
(xy)ᵃ = xᵃ* yᵃ
As you probably guessed, the same rule applies for division.
x³/ y³ = (x/y)³
And the “proof:”
x³ / y³ = (x * x * x) / (y * y * y) = (x/y) * (x/y) * (x/y) = (x/y)³
And finally, the generalized form of the rule, accompanied by the reversal:
xᵃ / yᵃ = (x/y)ᵃ
(x/y)ᵃ = xᵃ/ yᵃ
One more rule remains to be covered in this introduction. To preview it, let’s return to our idea of “splitting” an exponential expression into pieces:
x¹¹ = x⁷ * x⁴ = x⁶ * x⁵ = x¹⁰ * x
No one said that we have to limit ourselves to two “pieces.” We can keep “splitting” as many times as we want.
x¹¹ = x⁸ * x³ = x⁴ * x⁴ * x³ = x² * x² * x² * x² * x³
Here we see an x³ term multiplied by a string of four “x²” terms. But isn’t there a more efficient way to notate such a string of multiplications? Yes, with exponents! An exponential expression itself can become the base of another exponent.
x³ * x² * x² * x² * x² = x³ * (x²)⁴
Remember that our (x²)⁴ term started out as x⁸. This reveals the rule for simplifying “nested” exponential expressions, or what we call a “power to a power”:
(xᵃ)ᵇ = xᵃ * ᵇ
xᵃ * ᵇ = (xᵃ)ᵇ
This rule makes sense when you know that exponential expressions are “made of” successive multiplications. Four groups of two “x’s” in multiplication is the same thing as 8 “x’s” in multiplication. And you know the drill: the reversal of the rule – where a single exponent is factored to create a “nested” expression – is just as useful as the “original” version.
Now to assemble all of our rules:
xᵃ * xᵇ = x⁽ᵃ⁺ᵇ⁾
x⁽ᵃ⁺ᵇ⁾ = xᵃ + xᵇ
xᵃ / xᵇ = x⁽ᵃ⁻ᵇ⁾
x⁽ᵃ⁻ᵇ⁾ = xᵃ/ xᵇ
xᵃ * yᵃ = (xy)ᵃ
(xy)ᵃ = xᵃ * yᵃ
xᵃ / yᵃ = (x/y)ᵃ
(x/y)ᵃ = xᵃ/ yᵃ
(xᵃ)ᵇ = x⁽ᵃᵇ⁾
x⁽ᵃᵇ⁾ = (xᵃ)ᵇ
And before we try a few official GMAT problems, let’s take a look at some powers of integers you should know:

The main reason for knowing these powers is for something I call “backwards recognition.” If you don’t memorize these and you need to evaluate 54 or 27 in order to solve a problem, you can probably multiply your way through the powers easily enough. But it’s another thing to see 625 or 128 in a problem and immediately know “that’s 54” or “that’s 27.” Such backwards recognition can help you make sense of problems that may look confusing at first.
As a final reminder of the “power to a power” rule, powers of 4 are left out of this list because they are contained within the powers of 2. Every even power of 2 is also a power of 4. For example, 16 = 24 = 42, 64 = 26 = 43, so on and so forth.
Let’s try some official GMAT problems involving exponents. Here’s a simple one to get you started:
216 is
(A) 2 more than 2¹⁵
(B) 16 more than 2¹⁵
(C) ½ of 2³²
(D) 2 times 2⁸
(E) 2 times 2¹⁵
If you’ve gotten your head around exponents, this is a 15-second problem. Notice that answer choices C and D both imply the same incorrect rule: that doubling the exponent on the 2 doubles the overall value. Even if you don’t know your exponent rules, you could eliminate these answer choices on logic alone because they are indistinguishable. Answer B doesn’t make much sense, and answer A confuses the rules of exponents with the rules of multiplication. (2 * 16) is 2 more than (2 * 15), but the difference between 216 and 215 is much greater. Answer E gets it right. Increasing the value of the exponent by 1 means to multiply by the base one more time.
Here’s another:
At the start of an experiment, a certain population consisted of 3 animals. At the end of each month after the start of the experiment, the population was double its size at the beginning of that month. Which of the following represents the population size at the end of the 10 months?
(A) 2³
(B) 3²
(C) 2 * 3¹⁰
(D) 3 * 2¹⁰
(E) 3 * 10²
If you understood our example with the hens, this should be another easy one. We need to start with 3 and then double our value (multiply by 2) 10 times. Exponents enable us to notate this series of multiplications as 3 * 2¹⁰, answer choice D.
Now for some data sufficiency:
What is the value of 6ˣ 6ʸ ?
- 2⁽ˣ⁺ʸ⁾ = 32
- 3⁽ˣ⁺ʸ⁾ = 243
If you know your exponent rules, you should immediately note that 6x6y can be alternatively written as 6ˣ⁺ʸ. Since this is DS, you don’t necessarily need to know which power of 2 equals 32 or which power of 3 equals 243; it’s enough to recognize that each statement on its own locks in the value of the exponent “x + y” and therefore the value of the 6ˣ⁺ʸ expression that we were asked about. (But ideally you will study your powers enough to know right away that 32 = 2⁵ and 243 = 3⁵.) The correct answer choice is D.
Here’s our final problem for this article:
What is the smallest integer n for which 25ⁿ > 5¹²?
(A) 6
(B) 7
(C) 8
(D) 9
(E) 10
This is a case where backwards recognition of powers makes all the difference. 25 should be immediately recognizable as 52. Therefore the given inequality can be rewritten in either of the following ways:
(5²)ⁿ > 5¹²
25ⁿ > 5⁽²×⁶⁾ . . . 25ⁿ > (5²)⁶ . . . 25ⁿ > 25⁶
The second way gets you to the correct answer more quickly, but the first is rather more intuitive. The “power to a power” rule states that the exponents should be multiplied:
(5²)ⁿ > 5¹²
5²ⁿ > 5¹²
Plugging in a 6 makes the exponents equal (2 * 6 = 12), and since the bases are now equal, the expressions would be equal as well. Therefore the smallest integer that works is 7, answer choice B.
I hope you’ve enjoyed this intro to (or review of) exponent properties. As you will definitely come across exponents on the GMAT test, we think that this article is something you need to read carefully! Next time we’ll learn how to “undo” exponents with an inverse operation.
Undoing Exponents: Radicals and Roots
As you will definitively have to deal with radicals on the GMAT and Executive Assessment (EA), we’ve put together an article for you to master the topic. Addition is “undone” by subtraction, multiplication is “undone” by division, and the powers notated by exponents are “undone” with a piece of notation called a radical.
√ the radical
The number, variable, or expression inside or under the radical is referred to as the radicand, and sometimes there is a small number called the index nestled in the “crook” of the radical.
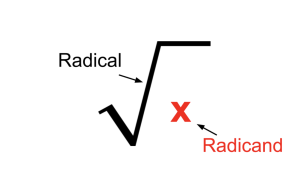
When no index appears, the index is understood to have a value of 2. (This will make sense momentarily.) Unfortunately there exists no one-word name – like “addition” or “multiplication” for what exponents do. For an exponent of n, we use the phrase “raising to the nth power.” For a radical with an index of n, we use the phrase “taking the nᵗʰ root.” Exponents notate powers, radicals notate roots. If there is an “invisible” index of 2, the notated value is called the square root of the radicand (the number inside or under the radical). If the index is 3, the notated value is called the cube root of the radicand. For all integers above 3, we use the usual ordinals (fourth root, fifth root, etc.)
√36 the square root of 36
³√125 the cube root of 125
⁴√81 the fourth root of 81
If you’ve studied your powers chart from the first article in this series, you should recognize those radicands. Here’s a simple way to represent how radicals “undo” exponents:
xⁿ = a ⁿ√a = x
If the nᵗʰ power of x equals a, then the nth root of a equals x. Radical expressions like this notate the number x which, when multiplied by itself n times (or, to use exponents, raised to the nᵗʰ power), equals a. Exponential expressions “start with” a base and raise it to a power, notating a value (in our case the variable a). Radical expressions “start with” the full value notated by some exponential expression and use the exponent from this expression as a root, notating the base of the exponential expression (in our case the variable x). To use our examples above:
√36 the square root of 36 x² = 36, x = 6
³√125 the cube root of 125 x³ = 125, x = 5
⁴√81 the fourth root of 81 x⁴ = 81, x = 3
Now you have another reason to learn your common powers: when you see one of those special numbers underneath a radical, you can quickly evaluate the radical expression. This is akin to how knowing your times tables makes division really easy.
Another quality of roots is that they can be “translated” into fractional exponents according to the following rule:
ⁿ√(xᵃ) = xᵃ⁄ⁿ
(ⁿ√x)ᵃ = xᵃ⁄ⁿ
Two forms are shown because the position of the exponent a is irrelevant. It can be considered “within” and “before” the radical operation as in the first version or “above” and “after” the radical operation as in the second version.
As always, this rule can be reversed.
xᵃ⁄ⁿ = n√(xa)
xᵃ⁄ⁿ = (n√x)a
Seeing fractional exponents written in GMAT and EA questions is quite rare, but sometimes a given radical expression that doesn’t break down easily is better notated as a fractional exponent for the sake of seeing potential algebraic simplifications.
This correlation between radicals and fractional exponents brings up the key point that radicals and exponents are just different – or reverse – ways of notating the same thing. Therefore all the exponent rules apply to radicals as well. The radical versions appear less frequently than the exponent versions but are still valuable pieces in your toolkit.
Equal bases with different roots are rather unusual; combining or collapsing roots with the same index is certainly more common. And just as we can have a “power of a power,” we can have a “root of a root.”
These rules bring up a final important point about radical expressions: they often need to be simplified. Mathematicians don’t like to leave numbers inside radicals when it is possible to express the same value differently, so many answer choices on the GMAT and EA involve simplified versions of radical expressions. Here’s an example for our purposes:
√630
We’ll have to get into some number properties to show what happens here. One of our radicals rules states that this radicand 630 can be broken into factors and represented as multiple radical expressions. Let’s break down 630 to its prime factors.
630 = 2 * 3² * 5 * 7
√630 = √(2 * 3² * 5 * 7)
Given an index of n, any n (number) of the same prime factor can be placed inside their own radical. Since we are taking a square root here (with an understood index of 2), we only need two of the same prime factor in order to do this. Here we can do it with our 3s.
√630 = √(2 * 3² * 5 * 7)
√630 = √(3²) * √(2 * 5 * 7)
Now the power of 2 and the root of 2 on the 3 cancel each other out.
√630 = √(32) * √(2 * 5 * 7)
√630 = 3 * √(2 * 5 * 7)
√630 = 3√70
When simplifying a radical expression, use the index as a key. Given an index of n, look for sets of n (number) of the same prime factor. For each of these sets, bring one of that prime factor out in front of the radical. Here’s another example:
³√8640
A key step to shortening the process is recognizing 216 as 63. Let’s line up our prime factors:
2⁶ * 3³ * 5
Remember that we’re taking a cube root this time, so we’re looking for sets of three of the same prime factor. We can make two sets from our 2s (since we have six of them) and one set from our 3s. So two 2s and one 3 come out from the radical, leaving only the 5.
³√8640 = 2 * 2 * 3 * ³√5 = 12³√5
To close this article, let’s try a couple of official GMAT problems involving radicals:
If n = √(16/81), What is the value of √n?
(A) 1/9
(B) 1/4
(C) 4/9
(D) 2/3
(E) 9/2
This problem benefits from knowing both your rules and your powers. Knowing your rules lets you represent this radical expression as √16/√81, and knowing your powers lets you easily recognize √16 as 4 and √81 as 9, leading to answer choice C, 4/9. Here’s one more:
In the formula w= P/√v, Integers p and t are positive constants. If w=2 when v=1 and if w=1/2 when v=64, then t=
(A) 1
(B) 2
(C) 3
(D) 4
(E) 16
First we are told that w = 2 when v = 1.
2 = P / ᵗ√1
Here you need to recognize a fact we haven’t mentioned yet: that any root (or power) of 1 is still 1. This makes sense when you think about multiplying 1 by itself again and again – the value never changes. Therefore the denominator of the expression equals 1, and P must equal 2. Armed with this knowledge, you can make use of the second given fact: w = ½ when v = 64.
½ = 2/ᵗ√64
4 = ᵗ√64
If you recognize 64 as 26, you can use your “power to a power” rule to change 26 to 43, leading you to answer choice C.
This concludes our survey of radicals on the GMAT and EA. Next time we will introduce negatives to exponential expressions.
Negative Exponents and Negative Bases
Welcome back to our series on exponents. Today we will see what happens when we throw negatives into our exponential expressions. We will explore both negative bases and negative exponents.
First, the bases. The rule to remember for negative bases is that odd powers of negative bases are negative and even powers of negative bases are positive. This rule makes sense when you remember that exponents simply notate a number of multiplications by the base (and remember your rules about multiplication with negative factors).
Multiplication with an odd number of negative factors yields a negative product:
(-x)3 = -x * -x * -x
(-x)3 < 0
Multiplication with an even number of negative factors yields a positive product:
(-x)4 = -x * -x * -x * -x
(-x)4 > 0
A note on notation: parentheses should always be used around a negative value as the base of an exponent. If they are not, then the order of operations dictates that the exponent be applied before the negative sign. To avoid confusion, whenever the negative is meant to be left out of the exponential operation, parentheses are used like this: -(x)4 to make the order clear. Please note that -(x)4 is less than 0, and (-x)4 is greater than 0.
Now for negative exponents. Here is a simple rule is the best way to explain it:
x-n = 1/xn
A negative exponent indicates a value reciprocal to the value with a positive exponent. It’s good practice to “translate” any exponential expressions with negative exponents to their reciprocal positive forms. Seeing it both ways can help you make sense of problems.
5-4 = 1 / (54) = 1 / 625
17-2 = 1 / (172) = 1 / 289
(9 / 16)-2 = (16 / 9)2 = 256 / 81
Integer bases with negative exponents go under a numerator of 1; fractional bases with negative exponents simply flip. Let’s look at some “double negative” exponential expressions.
(-6)-3 = 1 / (-6)3 = 1 / -216
(-2)-10 = 1 / (210) = 1 / 1024
(-4 / 3)-4 = (-¾)4 = 81 / 256
Let’s get into some official GMAT problems. Be careful with this first one!
From the consecutive integers -10 to 10 inclusive, 20 integers are randomly chosen with repetitions allowed. What is the least possible value of the product of the 20 integers?
(A) (-10)20
(B) (-10)10
(C) 0
(D) -(10)19
(E) -(10)20
One incorrect answer is chosen far more often than any other on this problem: answer choice D. Trying to minimize the product, many people consider taking the maximum number (20) of the lowest value (-10). The common mistake is then thinking that -(10)20 (answer choice E) is actually a positive value since it involves an even number (20) of negative factors. Many people then take “the next best thing” in answer choice D, which shifts the exponent to the next odd number down from 20.
In fact, -(10)20 does not involve an even number of negative factors, since the negative sign is excluded from the exponential expression by the parentheses. Answer E means “take 1020 and make it negative.” It is true that taking 20 negative tens and multiplying them all together produces a large positive value (the opposite of what we are aiming for on this problem), but this misguided idea is notated by answer choice A – not answer choice E. Remember that the answer choices notate the product of the 20 factors, not necessarily a condensed list of the 20 factors.
It is possible to choose 20 integers from -10 to 10 inclusive that, when multiplied, yield a product of -(10)20 (answer choice E). The “least possible value” is obtained by finding the greatest absolute value (distance from 0) in negative form. So we want all 20 of our factors to be either 10 or -10 since this will maximize the absolute value (distance from 0) of the product. To ensure that the product is also negative, we simply need an odd number of negative tens. We can use nineteen negative 10s and 1 positive 10, 1 negative 10 and 19 positive 10s, or any odd combination in between. Any of these options will yield a product of -(10)20. Read the notation carefully!
Let’s try another:
The value of 2(-14)+2(-15)+2(-16)+2(-17)/5 is how many time the value of 2(-17)?
(A) 3/2
(B) 5/2
(C) 3
(D) 4
(E) 5
This problem benefits from the skill of noticing patterns and “checking” them. You should see the pattern in the numerator and generalize it by saying “the negative exponent on the 2 keeps decreasing by 1.” Then you can see how this pattern “works” by checking a single case.
2-17 = 1 / 217
2-16 = 1 / 216
Since 217 = 2 * 216, (1 / 217) is half the value of (1 / 216). Or, to say it a more useful way, 2-16 = 2 * 2-17 This pattern will continue through the numerator. Since we are looking for how many copies of 2-17 we have in this expression, we can replace 2-17 with 1 and follow the pattern.
(2–14 + 2-15 + 2-16 + 2-17) / 3
(8 + 4 + 2 + 1) / 3
15 / 3 = 3
And the correct answer is C.
Here’s a final problem for today:
a is a nonzero integer. Is
a2greater than 1?
- a < -1
- a is even.
To evaluate statement 1, simply start by checking a = -2. (-2)-2 = 1 / (-2)2 = ¼. Moving on to a = -3, (-3)-3 = 1 / (-3)3 = 1 / -27. This time the value is negative, but the positive value from a = -2 is still less than 1. If you imagine continuing with a = -4, a = -5, etc., you will just keep making smaller and smaller fractions. Statement 1 alone is sufficient.
Statement 2 on its own is easy to check since we already know from checking statement 1 that some even values for the variable a yield an aa with a value less than 1. And it shouldn’t be hard to imagine an even value for variable a where aa is greater than 1. For example, 22 = 4 and 44 = 256. So statement 2 alone is insufficient, and the correct answer is A.
If you went with answer choice C, here’s what might have happened. Noticing that statement 1 tells you the base is negative, you might have seen next that statement 2 tells you the exponent is even. You might have thought that this “evenness” of the exponent makes the difference since it determines the positivity or negativity of the expression. Very often in DS problems with negative bases, the even/odd identity of the exponent really matters. But in this case, it’s a trap, because we were asked whether aa is greater than 1 (not 0), and the fact that the exponent is also negative means that it’s even/odd identity is irrelevant – the value is always less than 1.
The rules governing negative exponents and negative bases are simple, but the GMAT and EA problems that employ these rules can catch you if you aren’t careful. Next time we will look at another tricky exponential scenario: when the base is between -1 and 1.
Register now for a free consultation with one of our top tutors.
Bases Between -1 and 1
Many GMAT and Executive Assessment (EA) exponent problems – especially data sufficiency ones – require you to consider fractional bases. By this I mean proper fractions with values between -1 and 1, not improper fractions whose numerators exceed their denominators.
There are four “kinds” of bases separated by the three “boundary points” of -1, 0, and 1. Numbers in each of the four “zones” separated by these values behave similarly as bases of exponents. On many DS problems, we need to consider numbers less than -1, negative fractions, positive fractions, and numbers greater than 1, as well as the boundary points of -1, 0, and 1. This sounds like a lot of work, but practice will build your “spidey sense” for when a certain kind of base leads to an exception and an insufficient statement.
Let’s handle the “boundary points” first. As mentioned in a prior article, the boundary point of 1 is simple because it is “immune” to exponents: 1anything = 1. Likewise, 0positive = 0. For -1, (-1)even = 1 and (-1)odd = -1. Since (-1)anything equals either 1 or -1, it is worth noting that the absolute value of -1anything is 1. If you are unfamiliar with absolute value, don’t worry, it’s a simple concept: absolute value is a number’s distance from 0 on a number line. The absolute value of a positive number is . . . itself. The absolute value of a negative number is simply the positive version of the number. For positive numbers, “normal” value and absolute value are the same and trend together. For negative numbers, absolute value increases as “normal” value decreases. Absolute value is notated with vertical lines on either side of a value, variable, or expression. |(-1)anything| = 1.
Now for the four ranges of numbers. Numbers greater than 1 are the simplest. For these numbers, the higher the exponent, the higher the overall value. For numbers greater than 1, higher powers have higher values. Numbers less than -1 are only slightly more complex. For numbers less than -1, higher powers have higher absolute values, but odd powers are negative and even powers are positive.
Now for the positive and negative fractions: the more times you multiply a fraction by itself, the closer the resulting value gets to 0. (¾)2 or ¾ * ¾, which we can read as “¾ of ¾,” is less than ¾. For positive fractions, higher powers have lower values. For negative fractions, higher powers have lower absolute values, but odd powers are negative and even powers are positive.
Let’s demonstrate all of our rules with the examples of 2, -2, ½, and -½.
2 < 22 < 23 . . .
|2| < |22| < |23| . . .
(-2)5 < (-2)3 < (-2) < 0 < 22 < 24 < 26 . . .
|-2| < |(-2)2| < |(-2)3| . . .
½ > (½)2 > (½)3 . . .
|½| > |(½)2| > |(½)3| . . .
-½ < (-½)3 < (-½)5 < 0 < (-½)6 < (-½)4 < (-½)2
|-½| > |(-½)2| > |(-½)3| . . .
The patterns for the negatives can take some getting used to, so study these rules frequently and, more importantly, build your fluency with practice problems! Here’s a straightforward one:
Is x2 greater than?
- x2 is greater than 1.
- x is greater than -1.
For statement 1, it helps to remember that only numbers greater than 1 or less than -1 can have powers greater than 1. Powers of fractions are always fractions. So if x2 is greater than 1, x is either greater than 1 or less than -1. If x is less than -1, then x2, which according to the statement is greater than 1, is greater than x. And if x is greater than 1, it still gets larger when it is squared, so x2 is always greater than x, and statement 1 is sufficient.
Statement 2 tells us that x is greater than -1. If we remember our boundary points, we can solve this one without having to think about fractions. X could be 0 or 1, and in either case, x2 is equal to, not greater than, x. But for any number greater than 1, x2 is greater than x. So statement 2 on its own is insufficient, and the correct answer is A.
Let’s try another DS problem:
Is xy > x2y2?
- 0 < x2 < 1/4
- 0 < y2 < 1/9
To verbalize the question: is the absolute value of the product xy greater than the square of the product xy?
Statement 1 tells us that x2 is a positive fraction, which means that x itself is a fraction with a greater absolute value, but we don’t know whether it is positive or negative. Without knowing anything about y, this isn’t enough. Statement 1 alone is insufficient. Statement 2 is similar and also insufficient. Taking the statements together, we know that the absolute value of x is greater than x2, and the absolute value of y is greater than y2. It follows that the absolute value of the product xy is greater than x2y2. We don’t know whether x and y are positive or negative, but we’re talking absolute value so it doesn’t matter. The statements together are sufficient, and the correct answer is C.
Finally, let’s see what happens when fractional bases meet negative exponents:
(1/2)-3(1/4)-2(1/16)-1=
A. (1/2)(-48)
B. (1/2)(-11)
C. (1/2)(-6)
D. (1/8)(-11)
E. (1/8)(-6)
This problem benefits from “translating” out of the negative-exponent form. (½)-3 = 23, (¼)-2 = 42, and (1/16)-1 = 16. Ideally, you recognize that everything in the expression can be converted to powers of 2. 42 and 16 both equal 24, so the full expression is 23 * 24 * 24, or, remembering your exponent rules, 211. If you noticed how the fractional base and the negative exponent “canceled” each other, you should recognize 211 as (½)-11, answer choice B.
If you are looking for extra help in preparing for the GMAT, we offer extensive one-on-one GMAT tutoring for high-achieving students. You can schedule a complimentary, 30-minute consultation call with one of our tutors to learn more!
Exponent Properties in Data Sufficiency
Exponents have properties that make them ideal pieces for data sufficiency problems on the GMAT and Executive Assessment (EA) quant sections. We’ve surveyed most of these properties in our first four articles in this series, but a couple of key ones haven’t been mentioned explicitly.
First, x0 = 1. A full mathematical explanation of this property is beyond the scope of this series of articles and is unnecessary for GMAT/EA preparation. If you know the rule, you can employ it as needed. The debated exception 00 exists but does not occur on GMAT quant.
Second, the numbers 0 and 1 are both “immune” to exponents. We mentioned this rule for 1 in our last article, but it is important to know that the rule applies to 0 as well. 0x = 0, and 1x = 1.
Another important rule for exponent DS problems has already been mentioned: even powers of negative numbers are positive, and odd powers of negative numbers are odd. To extend this, xeven is always greater than or equal to 0 (it is only equal to 0 when x = 0; in all other cases xeven is positive).
A basic rule to remember is that positive numbers have two square roots which are negative and positive versions of the same value. If b2 = 16, b may equal 4 or -4. Forgetting about the possibility of the negative square root usually leads to incorrect answers.
One more important rule to remember is that if x is positive, then xy is positive. No exponent can cause an exponential expression with a positive base to have a negative value or a value of 0. To state the same rule differently, exponential expressions with negative values have negative bases.
Let’s get into some official problems:
Is zp negative?
- pz4 < 0
- p + z4 = 14
We will need to know the signs of the variables p and z. If they are both positive or both negative, then the product zp is positive. If z or p is negative and the other positive, then the product zp is negative.
Statement 1 tells us that the product p * z4 is negative. Therefore either of p or z4 is negative and the other is positive. Since the exponent 4 is positive, z4 is always positive (or 0, but the statement rules out that possibility). This means that p must be negative. This isn’t enough to answer whether zp is negative, but it may be useful if we have to combine statements 1 and 2.
Statement 2 tells us that the sum of p and z4 equals 14. There are simply too many possibilities for this statement on its own to be sufficient.
Now we must combine statements 1 and 2. We know from statement 1 that p is negative. Therefore z4 must be positive in order for p + z4 to have the positive sum of 14. But we already know that z4 is positive because the exponent 4 is even! A common mistake in these DS problems is to accidentally transfer information about z4 back to the variable z itself. Doing so on this problem might lead you to incorrect answer choice C. In this case, statements 1 and 2 together are still not sufficient, and the correct answer is E.
Let’s try another:
If r, s and t are nonzero integers is r5s3t4 negative?
- rt is negative.
- s is negative.
Here’s another even exponent of 4. This means that t4 is either positive, or 0 in the case of t = 0. If t = 0, then the product r5s3t4 is 0 and not negative.
Statement 1 tells us that the product rt is negative. Therefore either of r or t is negative and the other is positive. We still know nothing about the variable s, so this can’t be sufficient on its own.
Statement 2 tells us that s, and therefore s3, is negative, but it says nothing about r or t. This can’t be sufficient on its own.
Combining the statements, we can approach statement 1 with two pieces of info: that t4 is positive (or 0) and that s3 is negative (since s is negative). Therefore the product r5s3t4 is (?) * (-) * (+), and the sign of the variable r makes all the difference.
Returning to statement 1, we consider again that the product rt is negative. This means that either r or t is negative, but unfortunately, we don’t know which one. Again, if we mistakenly jump from the fact “t4 is positive” to the unfounded conclusion “t is positive,” we will select incorrect answer choice C. Again, the statements together are insufficient, and the correct answer is E.
Here’s another:
If a and b are integers is a5< 4b?
- a3= -27
- b2= 16
The upshot of statement 1 is that a is negative. Therefore a5 is also negative, since 5 is another negative exponent. To get specific (which is probably unnecessary for the problem), a = -3 and a5 = -243.
We don’t know anything about b, so it’s tempting to conclude that statement 1 alone is insufficient. But we are asked to compare a5 against 4b, not against b itself. If you remember the rule that exponential expressions with positive bases have positive values, you’ll see that statement 1 alone is sufficient. a5 is negative, and 4b is positive.
Statement 2 tells us that b = 4 or -4. Therefore 4b = 256 or 1/256. Either way, without statement 1, we know nothing about a5. Statement 2 on its own is insufficient, and the correct answer is A.
Here’s a final DS exponents problem:
If x and y are integers, is x > y?
- x + y > 0
- yx < 0
Statement 1 is certainly insufficient by itself, but we should still think about what it tells us. Either x and y are both positive, or one is negative and the other is positive, with the positive number having the greater absolute value.
Statement 2 tells us that yx is negative. The rule we need is that exponential expressions with negative values have negative bases. This means y is negative. On its own, this statement is still insufficient. But combined with statement 1, we know that x must be greater than y, because x must be positive in order to produce a positive sum with a negative number y. The statements together are sufficient, and the correct answer is C.
We are halfway through our series on exponents and have covered all the basics. The remaining five articles will cover specific problem types involving exponents.
If you are in the middle of studying for the GMAT and are looking for a private GMAT tutor, our elite tutors have all scored over 770 on the GMAT and have years of professional experience with tutoring. You can meet with us for a 30-minute complimentary consultation call.
Powers of 10 and Scientific Notation
Many GMAT and Executive Assessment (EA) exponents problems involve the use of 10 as a base. Since all the math we do is in a base 10 system, multiplying or dividing by powers of 10 simply moves the decimal point of a number. This enables us to notate very large and very small numbers with multiplication by powers of 10, a method called “scientific notation.” Problems featuring scientific notation are quite common on the GMAT and EA, although the tests do not use the term.
Let’s say you want to notate the 2019 GDP of the United States without using the word “trillion.” The value in question is 21.43 trillion dollars. A trillion is a million million and requires 12 zeros! (though here there are only 10 because of the .43)
21.43 trillion = 21,430,000,000,000
These zeros are getting a bit out of hand. Using scientific notation, we can represent the value this way:
2.143 * 1013
Conventions dictate that the coefficient be between 1 and 10, so we use 2.143 instead of 21.43 or 214.3. GMAT and EA questions will stick to this rule; all of the answer choices will be “proper” and correct or incorrect based on value alone, not style. Every multiplication by 10 effectively moves the decimal one place to the right, taking a new 0 on the number when necessary. It will take 13 of these moves to get back to the version of the “original” version of the number, so the exponent on the 10 in our notation is 13.
What if you want to tell someone how long light takes to travel 1 kilometer? The value is 0.0000033 seconds. The zeros are impressive, but we could simply write the number like this:
3.3 * 10-6
Since 10-1 = 1/10, multiplying by negative powers of 10 is the same thing as dividing by 10, which shifts the decimal point one place to the left. As before, zeros must be added to the number when we need them. In scientific notation, the decimal is 6 places to the right of where it would be in “normal” notation, so we need an exponent of -6 on the 10 to move the decimal back six places to the left.
Let’s try out some scientific notation problems:
A certain state’s milk production was 980 million pounds in 2077 and 2.7 billion pounds in 2014. Approximately how many million gallons of milk did the state produce in 2014 than in 2007? (1 billion = 109 and 1 gallon = 8.6 pounds.)
(A) 100
(B) 200
(C) 1,700
(D) 8,200
(E) 14,800
A certain state must have bought a lot of cows between 2007 and 2014. As we’ll see in the rest of our problems, many scientific notation problems on the GMAT and EA involve unit conversions – in this case from pounds to gallons. You’ll want to be familiar with the number of zeros indicated by million, billion, and trillion.
2.7 billion = 2.7 * 109
980 million = 9.8 * 108
The easiest way to handle operations with scientific notation is to work in columns. Deal with your coefficients and your powers of 10 separately, and convert back to “normal” notation as a final step when necessary. Since we are subtracting here (as indicated by the “how many more” phrase in the question), it makes sense to alter our scientific notation so that we are working with the same power of 10 in each number.
(2.7 * 109) – (9.8 * 108)
(27 * 108) – (9.8 * 108)
Technically we’ve “broken the rules” by using an exponent greater than 10 here, but that doesn’t matter. Now we can factor out the 108.
(27 * 108) – (9.8 * 108)
(27 – 9.8) * 108
17.2 * 108
This is still the difference in pounds, not gallons. To convert from pounds to gallons, we need to divide by 8.6. You may notice that 8.6 is exactly half of the 17.2 we’ve calculated. This is never coincidental and always a sign that you are on the right track.
(17.2 * 108) / 8.6
2 * 108
At this point, B must be the correct answer. Remember that the question asked us how many more million gallons were produced in 2014 than in 2007. That’s why the correct answer is 200, not 2 * 108.
2 * 108 = 200,000,000 = 200 million
Let’s try another:
A computer can perform 1,000,000 calculations per second. At this rate, how many hours will it take this computer to perform the 3.6 x 1011 calculations required to solve a certain problem?
(A) 60
(B) 100
(C) 600
(D) 1,000
(E) 6,000
Again, we have unit conversions. This time it is seconds to hours. GMAT and EA questions typically italicize units when conversions are involved to draw your attention to the shift.
If you know the seconds-to-hours conversion, this problem can be quite easy. There are 60 seconds in a minute and 60 minutes in an hour, so the number of seconds in an hour is 602 = 3600. This means that the computer in question performs 3600 * 1,000,000 calculations per hour.
(3.6 * 103) * (1 * 106) = 3.6 * 109
Switching to scientific notation and using your exponent rules to figure out the exponent on the 10 is generally better than writing out lots of zeros and hoping you count correctly. Observe that the number of calculations required to solve the “certain problem” we are asked about just happens to be 3.6 * 1011. This value is 100 times our calculated rate of 3.6 * 109 calculations per hour, so the correct answer is B, 100.
Let’s do just one more:
The age of certain granite rocks found in northwestern Canada is approximately 1.2 x 1017 seconds. Which of the following is closest to the age of these rocks, in years? (1 year is approximately 3.2 x 107 seconds.)
(A) 3.8 x 109
(B) 5.9 x 109
(C) 2.0 x 1010
(D) 2.0 x 1011
(E) 3.8 x 1011
Only in a GMAT/EA problem would anyone know the age in seconds of certain granite rocks found in northwestern Canada. Thankfully, this problem spares you the trouble of calculating the number of seconds in a year by supplying you with the value in scientific notation: 3.2 * 107.
The best way to perform division (or multiplication) on scientific notation values is to work “in columns,” taking the coefficients and the powers of 10 separately. Notice that your answer choices here stay in scientific notation, so converting to “normal” notation would just force you to switch back again at the end.
1.2 * 1017 / 3.2 * 107
1017 / 107 = 1010, but dividing 1.2 by 3.2 is somewhat less straightforward. If we recognize 0.4 as the greatest common factor of 1.2 and 3.2, we can see 1.2 / 3.2 as ⅜ or its decimal form: 0.375.
0.375 * 1010
Answers A and E both look good; they have simply moved the decimal one place to the right and rounded 3.75 to 3.8. But should the exponent be 9 (answer A) or 11 (answer E)? Since these answers involve moving the decimal one place to the right, it is now one place closer to where it would be in “normal” notation, and the correct change is shifting the exponent down to 9, not up to 11. The correct answer is A.
This concludes our foray into scientific notation. Next time we’ll see how powers of 10 can be used to notate numbers that are almost integers
Have you been studying for the GMAT and need a private tutor? Our elite tutors, who scored over 770 on the GMAT, offer 30 minutes of complimentary consultation time.
“Almost an Integer” Problems
Unless you do math as a career or a hobby, you probably prefer integers to non-integers. Whole numbers are easier for us to conceptualize. But a certain class of GMAT/Executive Assessment (EA) problems involves numbers that are almost integers. Generally, this nearest integer is 1, so the nearby numbers look like this:
0.99999
0.9995
1.001
1.000006
Whenever you see a number like one of these on a GMAT/EA problem, you should use powers of 10 to notate the difference between the value in question and the nearest integer.
Let’s start by expressing our first example number, 0.99999, as a difference from 1 without powers of 10. Then we’ll convert that difference to a power of 10.
0.99999 = 1 – 0.00001
When the number you’re working with is of the form 0.999 . . . , the difference from 1 is all zeros with a 1 at the end, and the number of digits after the decimal remains consistent. Here there are five nines after the decimal, so our difference from 1 has four zeros and then a 1 at the end for a total of five digits after the decimal.
Now to convert our difference from 1 to scientific notation. The number in question, 0.00001, is small, so the power of 10 will be negative. The rule is to simply use the negative version of the number of digits after the decimal. According to this rule, 0.00001 = 10-5. Therefore we have this:
0.99999 = 1 – 0.00001 = 1 – 10-5
Let’s try the next example from above: 0.9995. This time there are only four digits after the decimal, but the last one is a 5 instead of a 9. Again, let’s express this value as a difference from 1 without scientific notation first:
0.9995 = 1 – 0.0005
As before, the number of digits after the decimal must remain consistent. But instead of using all zeros and then a single 1, we use all zeros and then whatever digit sums to 10 with the final digit of the original number. When the final digit of the original number is a 9, as in the first example, we use a 1 (since 9 + 1 = 10). In this case, the final digit of the original number is 5, so we need to use another 5 (5 + 5 = 10) to finish off our difference from 1.
0.9995 = 1 – 0.0005 = 1 – 5*10-4
There are four digits after the decimal, so the exponent of the 10 is -4. The coefficient of 5 is applied to the 10-4 term because 0.0005 = 5 * 0.0001 = 5*10-4.
We can solidify this with a general rule for finding decimal differences from 1. The number of digits after the decimal must remain consistent, and the digits in each place must sum to 9, except for the final digits which sum to 10. Here’s an example:
0.8653 = 1 – 0.1347
Here are the sums of the tenths, hundredths, thousandths, and ten-thousandths digits:
8 + 1 = 9
6 + 3 = 9
5 + 4 = 9
3 + 7 = 10
Here are some numbers you can use for practice. Their differences from 1 are at the end of the article.
0.23468
0.9834
0.31479
0.34098
0.999357
0.00042
0.000257
This covers numbers slightly less than 1. Numbers slightly greater than 1, like the examples from before of 1.001 and 1.000006, are easier to work with because you can convert everything after the decimal directly to a power of 10 without having to find a difference from 1.
1.001 = 1 + 10-3
1.000006 = 1 + 6*10-6
With these skills in place, you’re ready to tackle some official problems.
(1.00001)(0.99999) – (1.00002)(0.99998) =
(A) 0
(B) 10-10
(C) 3(10-10)
(D) 10-5
(E) 3(10-5)
Let’s convert each of the four numbers in the problem:
1.00001 = 1 + 10-5
0.99999 = 1 – 10-5
1.00002 = 1 + 2*10-5
0.99998 = 1 – 2*10-5
And we have a lovely pattern emerging.
(1 + 10-5)(1 – 10-5) – (1 + 2*10-5)(1 – 2*10-5)
Now all that remains is to “foil” the expressions and then simplify:
(1 + 10-5)(1 – 10-5) – (1 + 2*10-5)(1 – 2*10-5)
(1 – 10-5 + 10-5 – 10-10) – (1 – 2*10-5 + 2*10-5 – 4*10-10)
Now all the 10-5 terms cancel:
(1 – 10-10) – (1 – 4*10-10)
Now the 1s cancel as well:
-(10-10) + 4(10-10)
3(10-10)
And the correct answer is C.
Here’s another:
1 – 0.00001 =
(A) (1.01)(0.99)
(B) (1.11)(0.99)
(C) (1.001)(0.999)
(D) (1.111)(0.999)
(E) (1.0101)(0.0909)
This one is different because the first step has already been done for us. Instead of starting with 0.999999, the problem starts in “difference from 1” form. All we have to do is convert the difference to a power of 10:
0.000001 = 10-6
1 – 0.000001 = 1 – 10-6
Now what to make of the answer choices? After a quick scan, the only ones that look very friendly to a “1 +/- 10-x” form are A and C. Choice A can’t be right because the factors 1.01 and 0.99 contain a total of only four digits after their decimals, and the product we are looking for, 1 – 10-6 or 0.999999, has six digits after the decimal. In multiplication, the number of digits after the decimal in the product always matches the total number of digits after the decimals in the factors.
So answer choice C looks like the best candidate. Let’s convert it to “power of 10” form:
(1.001)(0.999) = (1 + 10-3)(1 – 10-3)
Now we can “foil” the expression and simplify:
(1 + 10-3)(1 – 10-3) = 1 + 103 – 103 – 10-6 = 1 – 10-6
And as we suspected, answer choice C turned out to be correct.
Now you’re ready to handle “almost integers” on GMAT/EA problems. Next time we’ll use powers of 10 to address problems that ask about zeros or nonzero digits.
If you are looking for professional help to boost your GMAT/EA performance, head to our official website and book your 30 minutes complimentary assessment session now with our top tutors.
Solutions to drills:
0.23468 = 1 – 0.76532
0.9834 = 1 – 0.0166
0.31479 = 1 – 0.68521
0.34098 = 1 – 65912
0.999357 = 1 – 0.000643
0.00042 = 1 – 0.99958
0.000257 = 1 – 0.999743
Exponents: Power of k Problems
Welcome to the penultimate article in our series on exponents on the GMAT/Executive Assessment (EA). Today we explore a problem category in which exponents are used to notating the highest power of an integer by which a larger integer is divisible. GMAT/EA problems typically use the variable k in the place of this exponent. These problems involve exponents but are also in the realm of number properties. Exponents are useful for notating the numbers of prime factors of a given integer. Here’s an example:
4680
468 * 10
234 * 2 * 2 * 5
117 * 2 * 2 * 2 * 5
13 * 9 * 2 * 2 * 2 * 5
13 * 3 * 3 * 2 *2 * 2 * 5
23 * 32 * 5 * 13
Since exponents notate successive multiplications by the same number, we can use them to consolidate lists of prime factors and immediately see how many of each prime factor exists within a number like 4680.
13 * 3 * 3 * 2 *2 * 2 * 5
23 * 32 * 5 * 13
In this example, 23 is a factor of 4680, but 24 is not a factor of 4680 because 4680 has only three prime factors of 2. 32 is a factor of 4680, but 33 is not a factor of 4680 because 4680 has only two prime factors of 3. A GMAT/EA problem might ask something like this: “What is the greatest integer k for which 2k is a factor of 4680?” The answer to this problem would be 3.
Let’s take a look at an official problem:
If p is the product of the integers from 1 to 30, inclusive, what is the greatest integer k for which 3k is a factor of p?
(A) 10
(B) 12
(C) 14
(D) 16
(E) 18
This question effectively asks, “How many prime factors of 3 are in the number p?” The number p is “the product of the integers from 1 to 30 inclusive.” This is the verbalization of a piece of notation called the factorial. Factorials notate the multiplication of a positive integer by each positive integer less than itself. Here are some examples:
4! = 4 * 3 * 2 * 1
7! = 7 * 6 * 5 * 4 * 3 * 2 * 1
9! = 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1
To generalize the formula:
n! = n * (n – 1) * (n – 2) * . . . * 1
Because the 1 at the end of the multiplication does not affect the value, factorials are often “spelled out” without the 1 at the end of the list.
Obviously, 30! Is too large of a number for us to evaluate. As a general rule, finding the actual value of any factorial larger than 7! or so is a waste of time. We are almost always more interested in the factors contained within a factorial.
30! = 30 * 29 * 28 * . . . * 1
So how many prime factors of 3 are contained within (30!)? Well, numbers like 29 and 28 don’t contain any prime factors of 3, because these numbers are not multiples of 3. The only factors of 30! that contain prime factors of 3 are the multiples of 3.
30 27 24 21 18 15 12 9 6 3
Some of these factors themselves contain more than one prime factor of 3. 27 is 33, so it has 3 threes. 9 is 32, so it has 2 threes. And a sneaky one is 18, which is not a power of 3 but is 2 * 9, or 2 * 32. So 18 also has 2 threes.
We can tally up all our prime factors of 3 like this:
30 27 24 21 18 15 12 9 6 3
1 3 1 1 2 1 1 2 1 1
If we add up the values in the second row, we obtain an answer of 14 prime factors of 3 in the number (30!). The correct answer is C.
This approach works, but there is actually a more straightforward way involving division. Consider first that performing the division a/b is effectively a way of counting how many multiples of b are less than or equal to a. 80 / 10 = 8, so 8 multiples of 10 are less than or equal to 80. 70 / 14 = 5, so 5 multiples of 14 are less than or equal to 70. When a is not perfectly divisible by b, the quotient still gives the number of multiples of b that are less than or equal to a, and the remainder is irrelevant. 56 / 9 = 6 remainder 2, so there are 6 multiples of 9 less than or equal to 56).
How does this help us identify prime factors of 3 in a number like (30!)? Well, if we take the quotient of 30/3, we can see how many of the factors of 30! are multiples of 3. In this case, there are 10. So there are at least 10 prime factors of 3 in the number (30!). If we take the quotient of 30/9 (or 30/(32), we see that 3 of these 10 multiples of 3 are also multiples of 9. Each of these numbers (9, 18, and 27) contains another prime factor of 3 that we did not “count” when we performed the division 30/3. Finally, we need to take 30/27 (or 30/33) to see that one of our 3 multiples of 9 is also a multiple of 27. The number, of course, is 27 itself, which contains a third prime factor of 3 that we didn’t “count” when we performed the divisions 30/3 and 30/9.
quotient of 30 / 3 = 10
quotient of 30 / 9 = 3
quotient of 30 / 27 = 1
10 + 3 + 1 = 14 prime factors of 3 within 30!
To find the highest integer k for which nk is a factor of t!, add up the quotients of t/n, t/(n2), t/(n3) . . . for every power of n that is less than or equal to t.
Here’s one that requires some extra steps of algebra:
If n = 9! – 64, which of the following is the greatest integer k such that 3k is a factor of n?
(A) 1
(B) 3
(C) 4
(D) 6
(E) 8
This question effectively asks, “How many prime factors of 3 are in the number 9! – 64?”
Let’s start by viewing 9! and 64 in factored forms:
9! – 64
(9 * 8 * 7 * 6 * 5 * 4 * 3 * 2) – (6 * 6 * 6 * 6)
We can go one step further and break all the non-primes down to primes:
(9 * 8 * 7 * 6 * 5 * 4 * 3 * 2) – (6 * 6 * 6 * 6)
(3 * 3) * 23 * 7 * (2 * 3) * 5 * 22 * 3 * 2 – (24 * 34)
Since each factor of 6 in 64 is equal to (3 * 2), we can represent the group of 4 sixes as (24 * 34). Now to consolidate the rest:
(3 * 3) * 23 * 7 * (2 * 3) * 5 * 22 * 3 * 2 – (24 * 34)
(27 * 34 * 5 * 7) – (24 * 34)
The subtraction is preventing us from seeing how many threes are in the integer version of this number. We will have to extract a factor of (24 * 34), like this:
(27 * 34 * 5 * 7) – (24 * 34)
(24 * 34)[(23 * 5 * 7) – 1]
Now we can evaluate the bracketed expression in order to prime factorize again:
(24 * 34)[(23 * 5 * 7) – 1]
(24 * 34)[(8 * 5 * 7) – 1]
(24 * 34)[280 – 1]
(24 * 34)(279)
And we’ll break 279 down into prime factors:
(24 * 34)(279)
(24 * 34)(9 * 31)
(24 * 34)(32 * 31)
24 * 36 * 31
Finally we can see that there are 6 prime factors of 3 in the number 9! – 64, and the correct answer is D.
Here’s a final problem for today:
For the positive integers a, b, and k, ak| |b means that ak is a divisor of b but a(k+1) is not a divisor of b. If k is a positive integer and 2k| |72, then k is equal to
(A) 2
(B) 3
(C) 4
(E) 8
(D) 18
This problem uses a random symbol – two vertical lines – and then defines it for you. This is common practice on GMAT/EA problems and is simply a way to “disguise” the type of problem you’re looking at. Think about the way they’ve defined this symbol, and you’ll see that this problem is asking the same thing as our other examples: what is the greatest integer k for which 2k is a factor of 72? Or to put it even more simply: How many prime factors of 2 does 72 have?
72 = 8 * 9 = 23 * 32
There are 3 prime factors of 2 in 72, so the correct answer is B.
This concludes our brief study of the “power of k” problems on the GMAT/EA. Join us next time for the final article in our series on exponents to learn how to handle problems with impossibly large numbers like 287459.
If you are in the middle of studying for the GMAT/EA and are looking for a private GMAT tutor, our elite tutors have all scored over 770 on the GMAT and have years of professional experience with tutoring. You can meet with us for a 30-minute complimentary consultation call.
Large Exponents and The Units Digit
Welcome to the final article in our series on exponents. Some GMAT and Executive Assessment (EA) quant problems feature impossibly large numbers like 287459. These are problems that you simply can’t hope to solve without a key piece of knowledge that we call units digit cycles.
Units digit cycles are extrapolations of the fact that the units digit of a product is entirely determined by the units digits of its factors. Consider the multiplication of two five-digit numbers ending with 3 and 7, respectively:
_ _ _ _ 3
x _ _ _ _ 7
Since 3 * 7 = 21, the units digit of the product of these two numbers is 1. Here’s another example:
_ _ _ 6
x _ _ 4
Since 6 * 4 = 24, the units digit of the product of these two numbers is 4.
Now let’s look back at the powers chart from the very first article in this series:
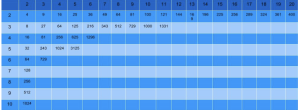
Hopefully, this chart is much more familiar to you now than it was when you read that first article. This time we’ve bolded the units digit of each value. Look down the 2 column, and you’ll see that the units digits follow the repeating cycle {2,4,8,6}. If we filled in a few more powers of 3, we could observe the repeating cycle {3,9,7,1}. For 5 and 6, the units digit never changes!
These cycles occur for powers of numbers because eventually, the units digit of a power of a given number will be the same as the units digit of the number itself. Let’s consider an example with the base 4. The units digit of 42 is determined by 4 * 4, which = 16. The units digit of 43 is determined by 6 * 4.
16
x 4
64
Since 6 * 4 = 24, the units digit of 43 is 4. Now the units digit of 44 is determined by 4 * 4, which is where we began when evaluating 42. Thus, the units digits of powers of 4 will simply alternate between 4 and 6. Since the series of powers of n is formed by successive multiplications by n, then whenever nk has units digit d, the units digit of nk + 1 is the units digit of d * n.
Here’s a full list of units digit cycles for the digits 0 through 9:
0: {0}
1: {1}
2: {2,4,8,6}
3: {3,9,7,1}
4: {4,6}
5: {5}
6: {6}
7: {7,9,1,3}
8: {8,4,2,6}
9: {9.1}
These cycles are a key piece of memorization for GMAT/EA quant. Let’s apply them to an official problem:
If n = 3343 + 4333, what is the units digit of n?
(A) 0
(B) 2
(C) 4
(D) 6
(E) 8
We’ll need to find and then add the units digits of 3343 and 4333. Remember that only the units digit of the base matters. The units digit of 3343 is the same as the units digit of 343. And the units digit of 4333 is the same as the units digit of 333.
The units digit of 343 is the units digit of the 43rd member of the cycle from above: {3,9,7,1}. The cycle repeats like this:
3 9 7 1 3 9 7 1 3 9 7 1 3 9 7 1 . . .
We don’t want to keep writing this all the way to the 43rd member, but we can use division as a shortcut. Divide the exponent by the number of members of the cycle for the units digit of the base, and the remainder of this division tells you which member of the cycle to take. The quotient of this division corresponds to the number of times you would count all the way through the cycle, which is irrelevant. The remainder tells you where in the cycle you “end up” when you reach the member you’re looking for.
In this case, our exponent is 43, and the units digit of our base is 3, which has a cycle with 4 members. So we need to divide 43 / 4 and take the remainder. Since the remainder of 43 / 4 is 3, the units digit of 343 (and of 3343) is the third member of the cycle {3,9,7,1}, which is 7.
Let’s run this again on the other value in the problem: 4333. Again the units digit of the base is 3, so we will use the cycle {3,9,7,1}. We still have four members in the cycle, so the remainder of the exponent divided by 4 tells us which member of the cycle to take. This time the exponent is 33. The remainder of 33/4 is 1, so we need the first member of the cycle {3,9,7,1}, which is 3.
As a final step in finding the units digit of 3343 + 4333, we need to add the units digits of 3343 and 4333, which we have found to be 7 and 3. Since 7 + 3 = 10, the units digit of 3343 + 4333 = 0. So the correct answer is A.
Some units digits problems ask about remainders. Here’s an example and the last official problem in our exponents series:
What is the remainder when 324 is divided by 5?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
When you see a very large exponent like 24, finding the units digit of the exponential expression is almost always required. We are working with a base of 3 again, so the units digit cycle is {3,9,7,1}. The exponent, 24, is a multiple of the number of members (4) of this cycle, so the remainder 24 / 4 is 0 and the units digit of 324 is the last member of the cycle: 1. So the number 324 has form _ _ _ _ _ 1. There are certainly more than 6 digits in 324, but all that matters here is the units digit. All multiples of 5 have units digits of 5 or 0, and a number with a units digit of 1 (like 324) is 1 greater than some number with a units digit of 0. Therefore the remainder of 324 / 5 is 1, and the correct answer is B.
This concludes our article on large exponents and the units digit, and our series of articles covering exponents on the GMAT and EA. If you missed any of the previous articles (there are 10 in total), search them out and read them through to strengthen your GMAT/EA quant readiness.
Are there any questions that you still have about the exponents on the GMAT/EA? Register now for a free 30-minute free consultation with one of our top tutors.
